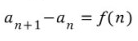33. [시간 및 상태] 종료되지 않은 반복문 재귀함수

안녕하세요 지에스인포입니다!

​

모두들 즐거운 나날 보내고 계신가요?

​

저희 정보보호 전문기업 (주)지에스인포는 7월에 들어서면서 매우 바빠지기 시작했는데요.

​

많은 직장인 분들이 휴가를 가시는 여름철에도 정보보안은 항상 철통같이 지켜져야 하기 때문이지요.

​

단 한 순간도 흐트러진 모습을 보이지 않고 한결같이 보안을 유지하는 것.

​

그것이 소중한 정보를 지키는 첫걸음이자 지에스인포의 모토이기도 하답니다!

​

그럼 오늘도 즐겁고 유익한 정보보안의 세계로 떠나볼까요?

​

오늘 배워 볼 항목은 행안부 SW 개발보안가이드의 33번째 항목인 '종료되지 않은 반복문 재귀함수' 입니다.

​

​

# 종료되지 않은 반복문 재귀함수 : 종료조건 없는 제어문 사용으로 반복문 또는 재귀함수가 무한히 반복되어 시스템의 자원을 고갈시키는 보안약점

​

여기서 재귀함수란?

-> 자기 자신을 호출하는 함수

​

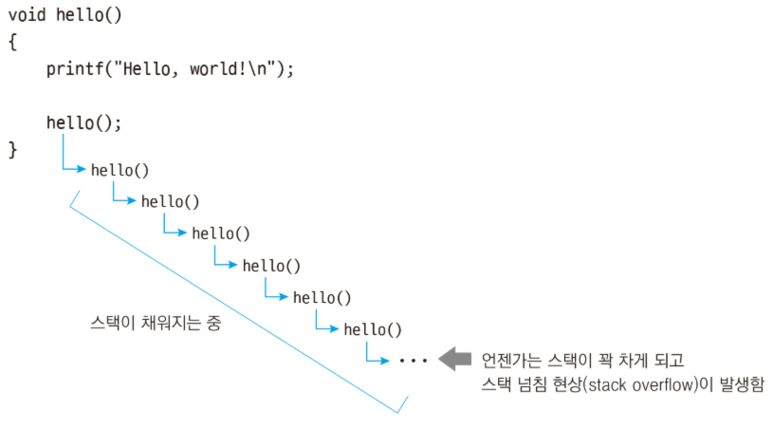
쉽게 이해하기 위해, 아래와 같이 hello(); 라는 이름을 가진 어떤 함수가 있다고 해 보겠습니다.

​

위 함수를 보면 hello()라는 함수를 호출했을 때, 그 안에서 또 hello() 함수를 호출하고 있지요?

​

이렇게 함수 안에서 자기 자신을 다시 호출하는 함수를 재귀함수라고 합니다. 영어로는 다시 돌아온다는 의미의 Recursive function 라고 하지요.

​

그러면 이러한 재귀함수의 문제점이 무엇일까요?

​

아래 그림을 함께 보시겠습니다.

​

​

위와 같이 hello() 함수 내부에서 또 hello() 함수를 호출하는 경우, hello() 함수가 작동되는 순간 프로그램은 hello ()안에서 끊임없이 hello()를 호출하는 무한루프의 늪에 빠지게 됩니다. 이렇게 될 경우 시스템 자원인 스택에 엄청난 과부하를 초래하게 되고, 언젠가는 스택이 꽉 차게 되어버려서 컴퓨터가 오작동을 일으키는 원인이 되는 것이죠.

​

그렇다면 이런 재귀함수를 왜 쓰는 것일까요?

​

바로 아래와 같은 재귀함수만의 장점이 있기 때문입니다.

1. 소스코드를 간단하게 줄일 수 있다.

2. 소스코드의 정확한 동작을 증명 할 수 있다.

3. 변수의 사용을 줄일 수 있다.

​

무슨 소리인지 이해가 안 되신다구요?

​

더 쉽게 말씀드리자면, 재귀함수의 경우에는 수학의 점화식과 같은 로직을 가지고 있습니다.

위와 같이, 함수의 값을 도출 할 때 앞서서 도출한 값이 다음 도출 값의 기준점이 되는 경우, 점화식을 사용해서 수학적인 표현을 할 수 있는데요.

바로 재귀함수가 이 점화식과 정확히 같은 기능을 하는 프로그램 로직이기 때문입니다.

​

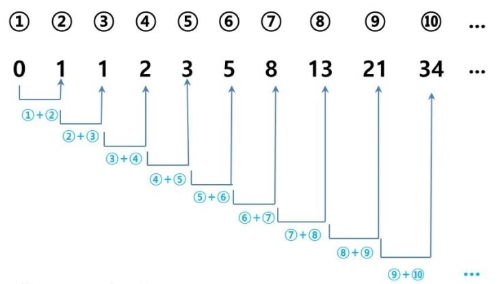
수열 중에 가장 유명하다고 알려져있는 피보나치 수열을 떠올리시면 이해가 쉬울 텐데요!

​

​

피보나치 수열은 앞의 두 수를 더한 값이 다음 수가 되는 규칙을 가진 수열입니다.

​

점화식으로는 f(n) = f(n-1) + f(n-2) 로 표현 할 수 있지요.

​

이것을 소스코드 알고리즘으로 표현하면 아래와 같이 나타낼 수 있는데요.

​

int fib(int n) {

if ( n <= 1 ) return 1;

else return fib(n-1) + fib(n-2)

}

​

함수 fib 안에서 또 fib를 호출하는 모습을 볼 수 있습니다.

​

이런 방식을 재귀(recursive) 함수라고 하는데요.

​

이와 같이, 알고리즘에서 앞의 변수 값이 다음 변수 값이 되거나, 혹은 다음 변수값을 도출하기 위한 함수의 기준값이 되는 경우 등 재귀함수를 써 주면 효율적으로 프로그램을 구현 할 수 있는 경우가 있

​

실제 소스코드 예시와 함께 보시겠습니다.

​

​

#프로그램 1

int sum = 0;

for(int i = 0; i <= 100; ++i){

sum += i;

}

printf("%d\n", sum);

​

#프로그램 2

int sum(const int x, const int acc) {

if(x > 100) return acc;

else return sum(x + 1, x + acc);

}

printf("%d\n", sum(0, 0));

​

​

위의 소스코드를 보시면, 둘 다 1부터 100까지의 합을 구현하는 알고리즘입니다.

​

그러나 프로그램 1의 경우에는 for문을 사용하여 해당 알고리즘을 수행하는 반면, 프로그램 2가 바로 재귀함수를 이용한 로직인데요. 보시면 결론은 똑같이 1부터 100까지의 합이 도출되지만 재귀함수를 사용한 프로그램 2의 경우에는 프로그램 1보다 도출 과정에서 변수(mutable state)의 사용을 적게 하고 있는 것을 볼 수 있는데요.

​

바로 이렇게 알고리즘에 있어서 변수의 사용을 줄이거나, 변수의 범위를 줄여주어서 안정적인 프로그램 로직을 수행하는데 재귀함수가 도움이 될 수 있다는 것입니다.

​

그렇다면 이 병주고 약주는 재귀함수를 어떻게 써야 할까요?

​

간단합니다. 재귀함수가 무한루프의 늪에 빠지지 않도록 탈출구를 잘 설계 해 주면 됩니다. 하늘이 무너져도 솟아날 구멍만 있으면 된다는 것이죠!

​

재귀함수 호출시 재귀 호출 회수를 제한하거나 초기값을 설정(상수)하여 재귀 호출을 제한하는 로직만 잘 구현하여 주면, 종료되지 않은 반복문 재귀함수 취약점을 예방 할 수 있습니다.

​

예시와 함께 보실까요?

​

위 소스코드는 재귀함수가 탈출문 없이 작성되어 한 번 실행되면 컴퓨터가 마비 될 때까지 무한히 호출되는 무한루프의 늪에 빠지게 됩니다.

​

​

반면, 위와 같이 재귀문을 빠져 나오는 조건인 귀납조건(Base case)를 구현 해 놓는다면 무한루프에 빠지지 않고서도 충분히 재귀문을 활용하여 프로그램이 잘 구동되도록 설계 할 수 있답니다!

​

참 쉽죠? ㅎㅎ 이렇게 간단한 로직 구현만으로도 보안상 치명적인 취약점을 미연에 방지 할 수 있다는 사실. 아는 것이 힘이다 라는 말이 느껴지는 항목이었습니다.

​

이상으로 '종료되지 않은 반복문 재귀함수 취약점'에 대한 글을 마치겠습니다.

​

다음에도 재밌고 유익한 보안 소식으로 찾아뵙겠습니다.